Кто сколько стоит. Ценность шахматных фигур. 14-ый шахматный урок.
Урок четырнадцатый. Кто сколько стоит. Ценность шахматных фигур.
Создано 23.06.2012 15:46
Автор: Костров В. и Давлетов Д.
Раз шахматы – это маленькая страна, в которой своя жизнь и своя война, то обязательно должна быть и своя шахматная валюта. Деньги должны быть лёгкими и удобными, и ты легко догадаешься, кто у нас самый лёгкий. Так сколько стоят шахматные фигуры и как определить ценность шахматных короля, ферзя, ладьи, слона, коня и пешки?
Среди огромных фигур на доске не сразу и заметишь маленькие шахматные пешки. Но именно они приняты за единицу измерения ценности фигур.
Пешка – это 1 шахматный рубль (деревянный) на шахматной доске.
Сколько стоят шахматные фигуры? Всё зависит от того, где эта фигура стоит, на сколько клеток она нападает.

Посмотри на позицию и сравни положение белого и чёрного коней. Белый атакует 8 полей, а чёрный лишь 2, к тому же ему некуда пойти – везде его съедят. Неравноценны у сторон и слоны. Чёрный не может ходить, а белый «посадил под замок» отряд чёрных фигур. Никакого значения не имеет лишняя чёрная ладья, её два хода бесполезны.
Сравним Их Величеств. У чёрного короля для передвижений несколько клеток, а белый – гуляет по всей доске. Понятно, что более свободные белые фигуры должны легко одержать победу.
Подвижность шахматной фигуры, а также способность её держать под ударом поля доски (Ударность) определяет её силу (
Проходные пешки приковывают к себе самые сильные фигуры противника. Но если пешка не может двигаться (блокирована) или сдвоена, то её цена сильно падает, почти до нуля.
Такой проворный, вёрткий конь, перепрыгивающий свои и чужие фигуры в начале партии, становится медленным и неуклюжим к её концу.
Зато ладья, которая из-за пешек никак не могла найти себе места в начале игры, выходит на свободу и становится очень сильной фигурой.
Ферзь в конце партии может справиться с целой армией фигур и пешек. А в начале он может запутаться в частоколе ног слабых фигур.
Силу фигур можно измерить только на пустой доске.
У них появляется Абсолютная сила.
Вспомним наши первые уроки – мы считали, что ферзь, стоящий в центре доски, держит под контролем 27(!) полей. Ладья может нападать лишь на 14. Можно сказать, что сила ферзя равна почти двум ладьям.
От количества полей, которые может контролировать каждая шахматная фигура, от количества направлений возможного движения, от скорости и маневренности зависит сила шахматной фигуры.
Но в зависимости от позиций, которые, как калейдоскоп, меняются в шахматной партии, изменяется и Относительная сила любой шахматной фигуры. Часто слабая фигура играет более важную роль по сравнению с сильной фигурой. Даже пешка может принести победу над самим ферзём.
Таблица силы и ценности шахматных фигур
|
Фигуры |
Кол-во ходов максим. |
Кол-во ходов миним. |
Направ. движения максим. |
Направ. движения миним. |
Сила фигуры |
|
(4) |
1 |
(3) |
1 |
1 |
|
|
8 |
2 |
8 |
2 |
|
|
|
13 |
7 |
4 |
1 |
3–3,5 |
|
|
14 |
14 |
4 |
2 |
|
|
|
27 |
21 |
8 |
3 |
10 |
|
|
8 |
3 |
8 |
3 |
4 (сила) |
Почему конь по силе примерно равен слону? Кажется, что слон более подвижен и бьёт гораздо больше полей на шахматной доске.
Но у слона есть один важный недостаток. Он может ходить лишь по полям одного цвета.
Король – это особая в шахматах фигура. Его ценность несравнима с ценностью даже всех фигур – с его потерей партия сразу заканчивается.
Поэтому шахматный король бесценен! Но он тоже имеет право вести бой. Король может закрыть путь трём пешкам. А в паре с пешкой он может доставить неприятности самым сильным фигурам.
Чтобы быстрее войти в шахматную жизнь нужно знать следующие равенства.
Если в процессе борьбы один из соперников обзавелся лишней фигурой или пешкой, то говорят, что у него материальное преимущество.
Если ты после борьбы поменял коня или слона на ладью, то у тебя лишнее качество.
Если ты поменял равноценные фигуры, например коня на слона, то считается, что произошел шахматный размен. А если после произошедших обменов у одной стороны не хватает до равенства материала, то произошёл неравноценный размен.
Использование данного материала в интернете без указания ссылки на автора, сайт и книгу запрещено. Правами на издание книги и данного материала владеют авторы шахматного учебника
Как научиться играть в шахматы? Список всех шахматных уроков онлайн.
С вопросами обращайтесь по адресу: Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.. Давайте уважать труд авторов, администраторов сайта и Детско-юношеской комиссии Санкт-Петербургской Шахматной Федерации.
Добавить комментарий
chessdeti.ru
Определяем веса шахматных фигур регрессионным анализом / Хабр
Здравствуй, Хабр!В этой статье речь пойдёт о небольшом программистском этюде на тему машинного обучения. Замысел его возник у меня при прохождении известного здесь многим курса «Machine Learning», читаемого Andrew Ng на Курсере. После знакомства с методами, о которых рассказывалось на лекциях, захотелось применить их к какой-нибудь реальной задаче. Долго искать тему не пришлось — в качестве предметной области просто напрашивалась оптимизация собственного шахматного движка.
Вступление: о шахматных программах
Не будем детально углубляться в архитектуру шахматных программ — это могло бы стать темой отдельной публикации или даже их серии. Рассмотрим только самые базовые принципы. Основными компонентами практически любого небелкового шахматиста являются поиск и оценка позиции.
Поиск представляет собой перебор вариантов, то есть итеративное углубление по дереву игры. Оценочная функция отображает набор позиционных признаков на числовую шкалу и служит целевой функцией для поиска наилучшего хода. Она применяется к листьям дерева, и постепенно «возвращается» к исходной позиции (корню) с помощью альфа-бета процедуры или её вариаций.
Строго говоря, настоящая
Поиск и оценка не существуют независимо друг от друга, они должны быть хорошо сбалансированы. Современные переборные алгоритмы давно уже не являются «тупым» перебором вариантов, они включают в себя многочисленные специальные правила, связанные в том числе и с оценкой позиции.
Первые такие усовершенствования поиска появились ещё на заре шахматного программирования, в 60-х годах XX в. Можно упомянуть, например, технику форсированного варианта (ФВ) — продление отдельных ветвей поиска до тех пор, пока позиция не «успокоится» (закончатся шахи и взаимные взятия фигур). Продления существенно увеличивают тактическую зоркость компьютера, а также приводят к тому, что дерево поиска становится очень неоднородным — длина отдельных ветвей может в несколько раз превышать длину соседних, менее перпективных. Другие улучшения поиска, наоборот, представляют собой отсечения или сокращения поиска — и здесь критерием отбрасывания плохих вариантов может, в числе прочего, служить всё та же статическая оценка.
Параметризация и улучшение поиска методами машинного обучения — отдельная интересная тема, но сейчас мы оставим её в стороне. Займёмся пока только оценочной функцией.
Как компьютер оценивает позицию
 Статическая оценка представляет собой линейную комбинацию различных признаков позиции, взятых с некоторыми весовыми коэффициентами. Какие это признаки? В первую очередь, количество фигур и пешек у той и другой стороны. Следующий важный признак — положение этих фигур, централизация, занятие дальнобойными фигурами открытых линий и диагоналей. Опыт показывает, что учёт только этих двух факторов — суммы материала и относительной ценности полей (зафиксированной в виде таблиц для каждого типа фигур) — при наличии качественного поиска уже может обеспечивать силу игры в диапазоне до 2000-2200 пунктов Эло. Это уровень хорошего первого разряда или кандидата в мастера.
Статическая оценка представляет собой линейную комбинацию различных признаков позиции, взятых с некоторыми весовыми коэффициентами. Какие это признаки? В первую очередь, количество фигур и пешек у той и другой стороны. Следующий важный признак — положение этих фигур, централизация, занятие дальнобойными фигурами открытых линий и диагоналей. Опыт показывает, что учёт только этих двух факторов — суммы материала и относительной ценности полей (зафиксированной в виде таблиц для каждого типа фигур) — при наличии качественного поиска уже может обеспечивать силу игры в диапазоне до 2000-2200 пунктов Эло. Это уровень хорошего первого разряда или кандидата в мастера.Дальнейшее уточнение оценки может включать всё более и более тонкие признаки шахматной позиции: наличие и продвинутость проходных пешек, близость фигур к позиции неприятельского короля, его пешечное прикрытие и т. д. Легендарная «Каисса», первая чемпионка мира среди программ (1974) имела оценочную функцию из нескольких десятков признаков. Все они подробно описаны в книге «Машина играет в шахматы», библиографическая ссылка на которую приводится в конце статьи.

Одна из самых «навороченных» оценочных функций была у машины Deep Blue, прославившейся своими матчами с Каспаровым в 1996-97 гг. (подробную историю этих матчей можно прочитать в недавней серии статей на Geektimes.)
Широко распространено мнение, что сила Deep Blue основывалась исключительно на колоссальной скорости перебора вариантов. 200 миллионов позиций в секунду, полный (без отсечений) перебор на 12 полуходов — к таким параметрам шахматные программы на современном железе только-только приближаются. Однако, дело было не только в быстродействии. По объёму «шахматных знаний» в оценочной функции эта машина также намного превосходила всех. Оценка Deep Blue была реализована аппаратно и включала до 8000 различных признаков. Для настройки её коэффициентов привлекались сильные гроссмейстеры (достоверно известно о работе с Джоэлем Бенджамином, тестовые партии с разными версиями машины играл Давид Бронштейн).
Не располагая такими ресурсами, как создатели Deep Blue, ограничим задачу. Из всех признаков позиции, учитываемых для подсчёта оценки, возьмём самый значимый — соотношение материала на доске.
Стоимость фигур: простейшие модели
Если взять любую шахматную книгу для начинающих, сразу за главой с объяснением шахматных ходов обычно приводится табличка сравнительной ценности фигур, примерно такая:
| Тип | Стоимость |
|---|---|
| Пешка | 1 |
| Конь | 3 |
| Слон | 3 |
| Ладья | 5 |
| Ферзь | 9 |
| Король | ∞ |
Приведённые стоимости фигур должны рассматриваться только как некоторые базовые ориентиры. В реальности фигуры могут «дорожать» и «дешеветь» в зависимости от ситуации на доске, а также от стадии партии. В качестве поправки первого порядка обычно рассматривают комбинации из двух-трёх фигур — своих и противника.
Вот как оценивал различные сочетания материала в своём классическом «Учебнике шахматной игры» третий чемпион мира Хосе-Рауль Капабланка:
С точки зрения общей теории слона и коня следует считать одинаково ценными, хотя, по моему убеждению, слон в большинстве случаев оказывается более сильной фигурой. Между тем считается вполне установленным, что два слона почти всегда сильнее двух коней.
Слон в игре против пешек сильнее коня, а вместе с пешками также оказывается более сильным против ладьи, нежели конь. Слон и ладья тоже сильнее коня и ладьи, но ферзь и конь могут оказаться сильнее, чем ферзь и слон. Слон часто стоит больше трех пешек, о коне же это редко можно сказать; он даже может оказаться слабее трех пешек.
Ладья по силе равна коню и двум пешкам или же слону и двум пешкам, но, как сказано выше, слон в борьбе против ладьи сильнее коня. Две ладьи несколько сильнее ферзя. Они немного слабее двух коней и слона и еще слабее двух слонов и коня. Сила коней падает по мере размена фигур на доске, сила же ладьи, напротив, возрастает.
Наконец, как правило, три легкие фигуры сильнее ферзя.
Оказывается, большей части подобных правил можно удовлетворить, оставаясь в рамках линейной модели, и просто слегка сместив стоимости фигур от их «школьных» значений. Например, в одной из статей приводятся следующие граничные условия:
B > N > 3P
B + N = R + 1.5P
Q + P = 2RИ значения, им удовлетворяющие:
P = 100
N = 320
B = 330
R = 500
Q = 900
K = 20000
Имена переменных соответствуют обозначениям фигур в английской нотации: P — пешка, N — конь, B — слон, R — ладья, Q — ферзь, K — король. Стоимости здесь и далее указаны в сотых долях пешки.
На самом деле, приведённый набор значений не является единственным решением. Более того, даже несоблюдение каких-то из «неравенств им. Капабланки» не приведёт к резкому падению силы игры программы, а только повлияет на её стилевые особенности.
В качестве эксперимента я провёл небольшой матч-турнир четырёх версий своего движка GreKo с разными весами фигур против трёх других программ — каждая из версий сыграла 3 матча по 200 партий со сверхмалым контролем времени (1 секунда + 0.1 сек. на ход). Результаты приведены в таблице:
| Версия | Пешка | Конь | Слон | Ладья | Ферзь | vs. Fruit 2.1 | vs. Crafty 23.4 | vs. Delfi 5.4 | Рейтинг |
|---|---|---|---|---|---|---|---|---|---|
| GreKo 12.5 | 100 | 400 | 400 | 600 | 1200 | 61.0 | 76.0 | 71.0 | 2567 |
| GreKo A | 100 | 300 | 300 | 500 | 900 | 55.0 | 69.0 | 73.0 | 2552 |
| GreKo B | 100 | 320 | 330 | 500 | 900 | 57.0 | 71.0 | 64.0 | 2548 |
| GreKo C | 100 | 325 | 325 | 550 | 1100 | 72.5 | 74.5 | 69.0 | 2575 |
«Классические» стоимости шахматного материала были получены интуитивно, путём осмысления шахматистами своего практического опыта. Предпринимались также попытки подвести под эти значения какую-то математическую базу — например, на основе мобильности фигур, числа полей, которые они могут держать под контролем. Мы же попробуем подойти к вопросу экспериментально — на базе анализа большого количества шахматных партий. Для вычисления стоимостей фигур нам не понадобится приближённая оценка позиций из этих партий — только их результаты, как самая объективная мера успеха в шахматах.
Материальный перевес и логистическая кривая
Для статистического анализа был взят PGN-файл, содержащий почти 3000 шахматных партий в блиц между 32 разными шахматными движками, в диапазоне от 1800 до 3000 пунктов Эло. С помощью специально написанной утилиты для каждой партии был составлен список материальных соотношений, возникших на доске. Каждое соотношение материала попадало в статистику не сразу после взятия фигуры или превращения пешки — сначала должны были произойти ответные взятия или несколько «тихих» ходов. Таким образом отфильтровывались краткосрочные «скачки материала» на 1-2 хода при разменах.
Затем по уже известной нам шкале «1-3-3-5-9» рассчитывался материальный баланс позиции, и для каждого его значения (от -24 до 24) накапливалось количество очков, набранных белыми. Полученная статистика представлена на следующем графике:
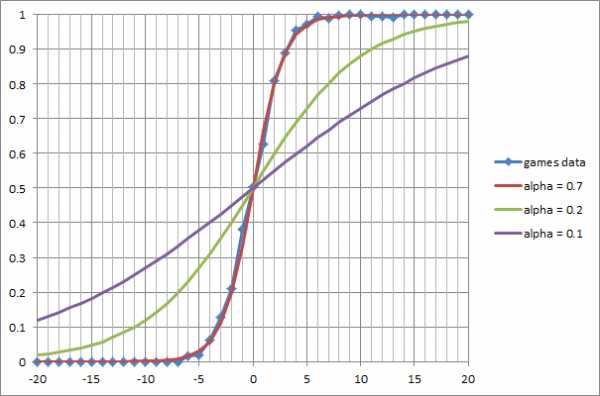
По оси x — материальный баланс позиции ΔM с точки зрения белых, в пешках. Он вычисляется как разность суммарной стоимости всех белых фигур и пешек и такой же величины для чёрных. По оси y — выборочное математическое ожидание результата партии (0 — победа чёрных, 0.5 — ничья, 1 — победа белых). Мы видим, что экспериментальные данные очень хорошо описываются логистической кривой:
Простой визуальный подбор позволяет определить параметр кривой: α=0.7, размерность его — обратные пешки.
Для сравнения на графике приведены ещё две логистические кривые с другими значениями параметра α.
Что это означает на практике? Пусть мы видим случайно выбранную позицию, в которой у белых перевес в 2 пешки (ΔM = 2). С вероятностью, близкой к 80%, мы можем утверждать: партия закончится победой белых. Аналогично, если у белых не хватает слона или коня (ΔM = -3), их шансы не проиграть всего лишь около 12%. Позиции с материальным равенством (ΔM = 0), как и можно было ожидать, чаще всего заканчиваются вничью.
Постановка задачи
Теперь мы готовы сформулировать задачу оптимизации оценочной функции в терминах логистической регрессии.
Пусть нам дан набор векторов следующего вида:
где Δi, i = P…Q — разность количества белых и чёрных фигур типа i (от пешки до ферзя, короля не считаем). Эти вектора представляют собой материальные соотношения, встретившиеся в партиях (одной партии обычно соответствует несколько векторов).
Пусть дан также вектор yj, компоненты которого принимают значения 0, 1 и 2. Эти значения соответствуют исходам партий: 0 — победа чёрных, 1 — ничья, 2 — победа белых.
Требуется найти вектор θ стоимостей фигур:
минимизирующий функцию стоимости для логистической регрессии:
,
где
— логистическая функция для векторного аргумента.
Для предотвращения «переобучения» и эффектов неустойчивости в найденном решении в функцию стоимости можно добавить параметр регуляризации, не дающий коэффициентам в векторе принимать слишком большие значения:
Величина коэффициента при параметре регуляризации выбирается небольшая, в данном случае использовалось значение λ=10-6.
Для решения задачи минимизации применим простейший метод градиентного спуска с постоянным шагом:
где компоненты градиента функции Jreg имеют вид:
Так как мы ищем симметричное решение, при материальном равенстве дающее вероятность исхода партии ½, нулевой коэффициент вектора θ полагаем всегда равным нулю, и нам для градиента нужно только второе из данных выражений.
Вывод приведённых формул мы здесь рассматривать не будем. Всем интересующимся их обоснованием настоятельно рекомендую уже упоминавшийся курс по машинному обучению на Coursera.
Программа и результаты
Так как первая часть задачи — разбор PGN-файлов и выделение для каждой позиции набора признаков — уже была практически реализована в коде шахматного движка, оставшуюся часть было решено также написать на C++. Исходный код программы и тестовые наборы партий в PGN-файлах доступны на github. Программа может быть собрана и запущена под Windows (MSVC) или Linux (gcc).
Возможность использовать в дальнейшем специализированные средства вроде Octave, MATLAB, R и т.п. также предусмотрена — в процессе работы программа генерирует промежуточный текстовый файл с наборами признаков и исходами партий, который легко может быть импортирован в эти среды.
Файл содержит текстовое представление набора векторов xj — матрицы размерности m x (n + 1), в первых 5 столбцах которой содержатся компоненты материального баланса (от пешки до ферзя), а в 6-м — результат партии.
Рассмотрим простой пример. Ниже приводится PGN-запись одной из тестовых партий.
[Event "OpenRating 31"]
[Site "BEAR-HOME"]
[Date "2013.05.09"]
[Round "1"]
[White "Simplex 0.9.7"]
[Black "IvanHoe 999946f"]
[Result "0-1"]
[TimeControl "60+1"]
[PlyCount "96"]
1. d4 d5 2. c4 e6 3. e3 c6 4. Nf3 Nd7 5. Nbd2 Nh6 6. e4 Bb4 7. a3 Ba5 8.
cxd5 exd5 9. exd5 cxd5 10. Qe2+ Kf8 11. Qb5 Nf6 12. Bd3 Qe7+ 13. Kd1 Bb6
14. Re1 Bd7 15. Qb3 Be6 16. Re2 Qc7 17. Qb4+ Kg8 18. Nb3 Bf5 19. Bb1 Bxb1
20. Rxb1 Nf5 21. Bd2 a5 22. Qa4 h6 23. Rc1 Qb8 24. Bxa5 Qf4 25. Qb4 Bxa5
26. Nxa5 Kh7 27. Nxb7 Rab8 28. a4 Ne4 29. h4 Rhc8 30. Ra1 Rc7 31. Qa3 Rcxb7
32. g3 Qc7 33. Rc1 Qa5 34. Rxe4 dxe4 35. Rc5 Qa6 36. Nd2 Nxd4 37. Rc4 Nb3
38. Nxb3 Qxc4 39. Nd2 Rd8 40. Qc3 Qf1+ 41. Kc2 Qe2 42. f4 e3 43. b4 Rc7 44.
Kb3 Qd1+ 45. Ka2 Rxc3 46. Nb1 Qxa4+ 47. Na3 Rc2+ 48. Ka1 Rd1# 0-1Соответствующий фрагмент промежуточного файла имеет вид:
0 0 0 0 0 0
1 0 0 0 0 0
2 0 0 0 0 0
2 -1 0 0 0 0
2 0 0 -1 0 0
1 0 0 -1 0 0
1 1 0 -2 0 0В 6-м столбце везде 0 — это результат партии, победа чёрных. В остальных столбцах — баланс числа фигур на доске. В первой строке полное материальное равенство, все компоненты равны 0. Вторая строка — лишняя пешка у белых, это позиция после 24-го хода. Обратим внимание, что предшествующие размены никак не отражены, они происходили слишком быстро. После 27-го хода у белых уже 2 лишних пешки — это строка 3. И т.д. Перед заключительной атакой чёрных у белых пешка и конь за две ладьи:
Как и размены в дебюте, финальные ходы в партии на содержимое файла не повлияли. Они были отсеяны «фильтром тактики», потому что представляли собой серию взятий, шахов и уходов от них.
Такие же записи создаются для всех анализируемых партий, в среднем получается по 5-10 строк на игру. После разбора PGN-базы с партиями этот файл поступает на вход второй части программы, занимающейся собственно решением задачи минимизации.
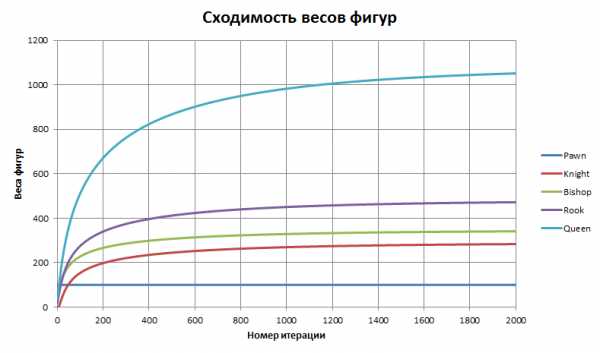
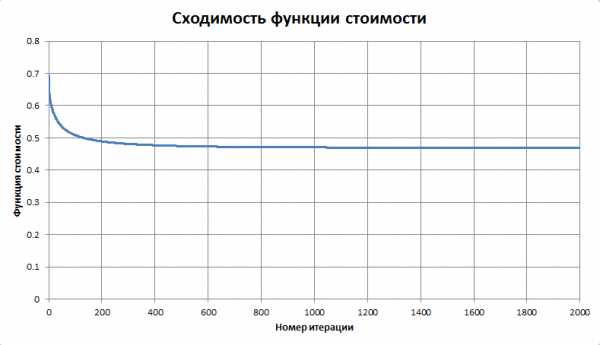
В качестве начальной точки для градиентного спуска можно, например, взять вектор со значениями весов фигур из учебника. Но интереснее не давать алгоритму никаких подсказок, и стартовать из нуля. Оказывается, наша функция стоимости достаточно «хорошая» — траектория быстро, за несколько тысяч шагов, выходит на глобальный минимум. Как изменяются при этом стоимости фигур, показано на следующем графике (на каждом шаге выполнялась нормировка на вес пешки = 100):
Текстовый вывод программы
C:\CHESS>pgnlearn.exe OpenRating.pgn
Reading file: OpenRating.pgn
Games: 2997
Created file: OpenRating.mat
Loading dataset...
[ 20196 x 5 ]
Solving (gradient method)...
Iter 0: [ 0 0 0 0 0 ] -> 0.693147
Iter 1000: [ 0.703733 1.89849 2.31532 3.16993 6.9148 ] -> 0.470379
Iter 2000: [ 0.735853 2.08733 2.51039 3.47418 7.7387 ] -> 0.469398
Iter 3000: [ 0.74429 2.13676 2.56152 3.55386 7.95879 ] -> 0.46933
Iter 4000: [ 0.746738 2.15108 2.57635 3.57697 8.02296 ] -> 0.469324
Iter 5000: [ 0.747467 2.15535 2.58077 3.58385 8.0421 ] -> 0.469324
Iter 6000: [ 0.747685 2.15663 2.58209 3.58591 8.04785 ] -> 0.469324
Iter 7000: [ 0.747751 2.15702 2.58249 3.58653 8.04958 ] -> 0.469324
Iter 8000: [ 0.747771 2.15713 2.58261 3.58672 8.0501 ] -> 0.469324
Iter 9000: [ 0.747777 2.15717 2.58265 3.58678 8.05026 ] -> 0.469324
Iter 10000: [ 0.747779 2.15718 2.58266 3.58679 8.0503 ] -> 0.469324
PIECE VALUES:
Pawn: 100
Knight: 288.478
Bishop: 345.377
Rook: 479.66
Queen: 1076.56
Press ENTER to finishПосле нормировки и округления получаем следующий набор величин:
| Тип | Стоимость |
|---|---|
| Пешка | 100 |
| Конь | 288 |
| Слон | 345 |
| Ладья | 480 |
| Ферзь | 1077 |
| Король | ∞ |
| Соотношение | Численные значения | Выполняется? |
|---|---|---|
| B > N | 345 > 288 | да |
| B > 3P | 345 > 3 * 100 | да |
| N > 3P | 288 < 3 * 100 | нет |
| B + N = R + 1.5P | 345 + 288 ~= 480 + 1.5 * 100 | да (с погрешностью < 0.5%) |
| Q + P = 2R | 1077 + 100 > 2 * 480 | нет |
Можно ли полученные значения использовать для усиления игры программы? Увы, на данном этапе ответ отрицательный. Тестовые блиц-матчи показывают, что сила игры GreKo от использования найденных параметров практически не изменилась, а в ряде случаев даже снизилась. Почему так произошло? Одна из очевидных причин — уже упоминавшаяся тесная связь поиска и оценки позиции. В поиске движка заложен целый ряд эвристик для отсечения неперспективных ветвей, и критерии этих отсечений (пороговые значения) тесно завязаны на статическую оценку. Меняя стоимости фигур, мы резко сдвигаем масштаб величин — форма дерева поиска меняется, требуется новая балансировка констант для всех эвристик. Это достаточно трудоёмкая задача.
Эксперимент с партиями людей
Попробуем расширить наш эксперимент, рассмотрев игры не только компьютеров, но и людей. В качестве массива данных для обучения возьмём партии двух выдающихся современных гроссмейстеров — чемпиона мира Магнуса Карлсена и экс-чемпиона Ананда Вишванатана, а также представителя романтических шахмат XIX столетия Адольфа Андерсена.

Ананд и Карлсен соперничают за мировую корону
В таблице ниже представлены результаты решения регрессионной задачи для партий этих шахматистов.
| Ананд | Карлсен | Андерсен | |
|---|---|---|---|
| Пешка | 100 | 100 | 100 |
| Конь | 216 | 213 | 286 |
| Слон | 230 | 243 | 289 |
| Ладья | 355 | 352 | 531 |
| Ферзь | 762 | 786 | 1013 |
| Король | ∞ | ∞ | ∞ |
Надо сказать, что похожая картина наблюдается не только у Виши и Магнуса, но и для большинства гроссмейстеров, партии которых удалось протестировать. Причём какой-то зависимости от стиля не выяснилось. Значения смещены от классических в одну и ту же сторону и у позиционных мастеров вроде Михаила Ботвинника и Анатолия Карпова, и у атакующих шахматистов — Михаила Таля, Юдит Полгар…
Одним из немногих исключений стал Адольф Андерсен — лучший европейский игрок середины XIX века, автор знаменитой «вечнозелёной партии». Вот для него значения стоимости фигур оказались очень близки к тем, которые используют компьютерные программы. Напрашиваются самые разнообразные фантастические гипотезы, вроде тайного читерства немецкого маэстро через портал во времени… (Шутка, конечно. Адольф Андерсен был крайне порядочным человеком, и никогда бы себе такого не позволил.)

Адольф Андерсен (1818-1879),
человек-компьютер
Почему наблюдается такой эффект со сжатием диапазона стоимости фигур? Конечно, не стоит забывать о крайней ограниченности нашей модели — учёт дополнительных позиционных факторов мог бы внести существенные коррективы. Но, возможно, дело в слабой технике реализации человеком материального перевеса — относительно современных шахматных программ, конечно. Проще говоря, человеку тяжело безошибочно играть ферзём, потому что у того слишком много возможностей. Вспоминается хрестоматийный анекдот о Ласкере (в других вариантах — Капабланке / Алехине / Тале), якобы игравшем с форой со случайным попутчиком в поезде. Кульминационной фразой было: «Ферзь только мешает!»
Заключение
Мы рассмотрели один из аспектов оценочной функции шахматных программ — стоимость материала. Убедились, что эта часть статической оценки в модели Шеннона имеет вполне «физический» смысл — она гладким образом (через логистическую функцию) связана с вероятностью исхода партии. Затем рассмотрели несколько распространённых комбинаций весов фигур, и оценили порядок их влияния на силу игры программы.
С помощью аппарата регрессии на партиях различных шахматистов, как живых так и компьютерных, мы определили оптимальные стоимости фигур в предположении чисто материальной оценочной функции. Обнаружили интересный эффект меньшей стоимости материала для людей по сравнению с машинами, и «заподозрили в читерстве» одного из шахматных классиков. Попробовали применить найденные значения в реальном движке и… не добились особого успеха.
Куда двигаться дальше? Для более точной оценки позиции можно добавлять в модель новые шахматные знания — то есть увеличивать размерность векторов x и θ. Даже оставаясь в области только материальных критериев (без учёта полей, занимаемых фигурами на доске), можно добавить целый ряд релевантных признаков: два слона, пара из ферзя и коня, пара из ладьи и слона, разноцвет, последняя пешка в эндшпиле… Шахматистам хорошо известно, как ценность фигур может зависеть от их сочетания или стадии партии. В шахматных программах соответствующие веса (бонусы или штрафы) могут достигать десятых долей пешки и более.
Один из возможных путей (наряду с увеличением размера выборки) — использовать для обучения партии, сыгранные предыдущей версией той же самой программы. В таком случае есть надежда на бóльшую согласованность одних признаков оценки с другими. Можно также в качестве функции стоимости использовать не успех предсказания исхода партии (которая может закончиться через несколько десятков ходов после рассматриваемой позиции), а корреляцию статической оценки с динамической — т.е. с результатом альфа-бета поиска на определённую глубину.
Однако, как уже было отмечено выше, для непосредственного усиления игры программы полученные результаты могут оказаться непригодными. Часто случается так: после обучения на сериях тестов программа начинает лучше решать тесты (в нашем случае — предсказывать результаты партий), но не лучше играть! В настоящее время в шахматном программировании мейнстримом стало интенсивное тестирование исключительно в практической игре. Новые версии топ-движков перед выпуском тестируются на десятках и сотнях тысяч партий со сверхкороткими контролями времени…
В любом случае, я планирую провести ещё ряд экспериментов по статистическому анализу шахматных партий. Если данная тема представляет интерес для аудитории Хабра, при получении каких-либо нетривиальных результатов статья может получить продолжение.
В ходе исследований ни одна шахматная фигура не пострадала.
Библиография
Адельсон-Вельский, Г.М.; Арлазаров, В.Л.; Битман, А.Р. и др. — Машина играет в шахматы. М.: Наука, 1983
Книга авторов советской программы «Каисса», подробно описывающая как общие алгоритмические основы шахматных программ, так и конкретные детали реализации оценочной функции и поиска «Каиссы».
Корнилов Е. — Программирование шахмат и других логических игр. СПб.: БХВ-Петербург, 2005
Более современная и «практическая» книга, содержит большое количество примеров кода.
Feng-hsiung Hsu — Behind Deep Blue. Princeton University Press, 2002
Книга одного из создателей шахматной машины Deep Blue, в подробностях рассказывающая об истории её создания и внутреннем устройстве. В приложении приведены тексты всех шахматных партий, сыгранных Deep Blue в официальных соревнованиях.
Ссылки
Chessprogramming Wiki — обширная коллекция материалов по всем теоретическим и практическим аспектам шахматного программирования.
Machine Learning in Games — сайт, посвящённый машинному обучению в играх. Содержит большое количество научных статей по исследованиям в области шахмат, шашек, го, реверси, нардов и т.д.
Kaissa — страница, посвящённая «Каиссе». Детально представлены коэффициенты её оценочной функции.
Stockfish — сильнейшая на сегодня программа, с открытым исходным кодом.
A comparison of Rybka 1.0 beta and Fruit 2.1
Детальное сравнение внутреннего устройства двух популярных шахматных программ.
GreKo — шахматная программа автора статьи.
Была использована в качестве одного из источников тестовых компьютерных партий. Также на основе её генератора ходов и парсера PGN-нотации была изготовлена утилита для анализа экспериментальных данных.
pgnlearn — код утилиты и примеры файлов с партиями на github.
habr.com
Урок четырнадцатый. Кто сколько стоит. Ценность шахматных фигур.
Раз шахматы – это маленькая страна, в которой своя жизнь и своя война, то обязательно должна быть и своя шахматная валюта. Деньги должны быть лёгкими и удобными, и ты легко догадаешься, кто у нас самый лёгкий. Так сколько стоят шахматные фигуры и как определить ценность шахматных короля, ферзя, ладьи, слона, коня и пешки?
Среди огромных фигур на доске не сразу и заметишь маленькие шахматные пешки. Но именно они приняты за единицу измерения ценности фигур.
Пешка – это 1 шахматный рубль (деревянный) на шахматной доске.
Сколько стоят шахматные фигуры? Всё зависит от того, где эта фигура стоит, на сколько клеток она нападает.

Посмотри на позицию и сравни положение белого и чёрного коней. Белый атакует 8 полей, а чёрный лишь 2, к тому же ему некуда пойти – везде его съедят. Неравноценны у сторон и слоны. Чёрный не может ходить, а белый «посадил под замок» отряд чёрных фигур. Никакого значения не имеет лишняя чёрная ладья, её два хода бесполезны.
Сравним Их Величеств. У чёрного короля для передвижений несколько клеток, а белый – гуляет по всей доске. Понятно, что более свободные белые фигуры должны легко одержать победу.
Подвижность шахматной фигуры, а также способность её держать под ударом поля доски (Ударность) определяет её силу (Ценность).
Проходные пешки приковывают к себе самые сильные фигуры противника. Но если пешка не может двигаться (блокирована) или сдвоена, то её цена сильно падает, почти до нуля.
Такой проворный, вёрткий конь, перепрыгивающий свои и чужие фигуры в начале партии, становится медленным и неуклюжим к её концу.
Зато ладья, которая из-за пешек никак не могла найти себе места в начале игры, выходит на свободу и становится очень сильной фигурой.
Ферзь в конце партии может справиться с целой армией фигур и пешек. А в начале он может запутаться в частоколе ног слабых фигур.
Силу фигур можно измерить только на пустой доске.
У них появляется Абсолютная сила.
Вспомним наши первые уроки – мы считали, что ферзь, стоящий в центре доски, держит под контролем 27(!) полей. Ладья может нападать лишь на 14. Можно сказать, что сила ферзя равна почти двум ладьям.
От количества полей, которые может контролировать каждая шахматная фигура, от количества направлений возможного движения, от скорости и маневренности зависит сила шахматной фигуры.
Но в зависимости от позиций, которые, как калейдоскоп, меняются в шахматной партии, изменяется и Относительная сила любой шахматной фигуры. Часто слабая фигура играет более важную роль по сравнению с сильной фигурой. Даже пешка может принести победу над самим ферзём.
Таблица силы и ценности шахматных фигур
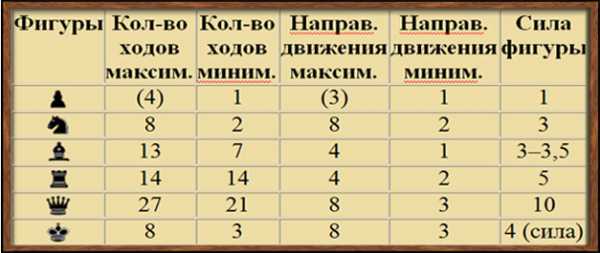
Почему конь по силе примерно равен слону? Кажется, что слон более подвижен и бьёт гораздо больше полей на шахматной доске.
Но у слона есть один важный недостаток. Он может ходить лишь по полям одного цвета.
Король – это особая в шахматах фигура. Его ценность несравнима с ценностью даже всех фигур – с его потерей партия сразу заканчивается.
Поэтому шахматный король бесценен! Но он тоже имеет право вести бой. Король может закрыть путь трём пешкам. А в паре с пешкой он может доставить неприятности самым сильным фигурам.
Чтобы быстрее войти в шахматную жизнь нужно знать следующие равенства.
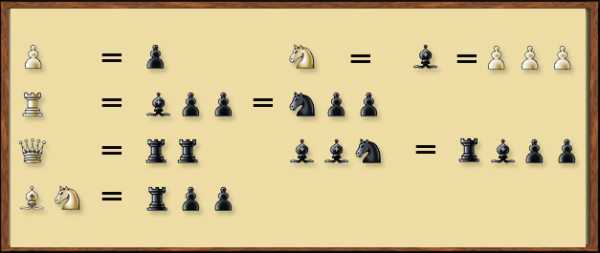
Если в процессе борьбы один из соперников обзавелся лишней фигурой или пешкой, то говорят, что у него материальное преимущество.
Если ты после борьбы поменял коня или слона на ладью, то у тебя лишнее качество.
Если ты поменял равноценные фигуры, например коня на слона, то считается, что произошел шахматный размен. А если после произошедших обменов у одной стороны не хватает до равенства материала, то произошёл неравноценный размен.
Шахматные уроки (оглавление)
www.72chess.com
Ценность фигур в шахматах – сколько пешек
 Стратегия игры в шахматы
Стратегия игры в шахматы
Три основных принципа шахматной партии.
1. Вести анализ и оценку позиции.
2. Составлять план действий.
3. Изыскивать комбинации и непрерывно вести расчет вариантов.
Для повышения мастерства нужно постоянно развивать и укреплять свои способности: решать шахматные задачи, анализировать чужие партии.
Рекомендации по розыгрышу дебюта
1. Главное — вывести с первоначальных мест все свои фигуры и расставить их на лучшие позиции, одновременно препятствуя сделать то же противнику. Следить за гармоничностью расстановки фигур: не делать ходы одной и той же фигурой; не делать много ходов пешками, задерживая вывод фигур; позаботиться о безопасности короля. Если противник отстал в развитии уже в начале партии, необходимо принять срочные меры, чтобы он и дальше не смог бы закончить вывод своих фигур с первоначальных мест, рокировать короля и т.д. Для этого надо связать противника необходимостью немедленной конкретной борьбы на одном из участков фронта. Вынужденный бросить туда свои силы, он не успеет закончить развитие фигур и не осуществит рокировку.
2. Проблему центра решать исходя из анализа. Если оценка позиции говорит о необходимости занимать центр пешками, надо занимать, если же пешкам грозит опасность стать слабыми и незащищенными, нужно все тщательно взвесить и, вероятно, предпочесть фигурное давление на центр.
3. Следить за пешечным построением.
Сколько фигур в шахматах?
Пешки назад не ходят, каждое ослабление одной пешки или всего пешечного расположения — это уже до конца партии.
4. Развивая фигуры, борясь за центр, создавая намеченные заранее пешечные построения , ни на минуту нельзя забывать общей идеи варианта. Любой дебютный вариант преследует цель выполнить одну или несколько задач. Наметив задачу, ее надо проводить, руководствуясь ею в проведении планов, подчиняя ей движение пешек и фигур.
Правила Стейница
1. Право атаковать в шахматах имеет сторона, владеющая преимуществом, и должна атаковать, иначе рискует растерять свое преимущество. Атака ведется на самый слабый пункт в позиции неприятеля.
2. Защищающийся должен отражать удары неприятеля, следовать его мысли, угадывать его намерения, но в то же время не упускать случая провести встречный удар, перейти в нужный момент в контратаку. Защита — временное подчинение воле противника. Защищаться труднее, чем атаковать.
3. В равных позициях стороны маневрируют, стремясь изменить равновесие в свою пользу. При правильной игре сторон, равная позиция вновь приводит к равным позициям.
4. Преимущество может состоять из одного большого неделимого преимущества и из ряда мелких преимуществ. Задача ведущего позиционный бой — накапливать мелкие преимущества, стремясь превратить временные преимущества в постоянные.
Постоянные преимущества и недостатки: материальный перевес, плохая позиция короля, наличие проходной пешки, слабые пешки, слабые поля, слабость периферии (для белопольного или чернопольного слона), пешечные островки, сильный пешечный центр, преимущество двух слонов, владение открытой вертикалью, владение открытой диагональю, владение горизонталью.
Временные преимущества и недостатки: неудачная позиция одной фигуры, дисгармония в расположении фигур, перевес в развитии, фигурное давление в центре, перевес в пространстве.
Правила при игре с разносторонними рокировками
1. Учесть, что противник почти обязательно бросится штурмовать вашу позицию на другом конце доски. Вопрос стоит: кто кого? Нужно твердо помнить, что успеха достигнет тот, кто первым захватит инициативу и заставит противника перейти к обороне, после чего все его активные действия на другом конце доски станут бессмысленными.
2. Предусмотреть, чтобы противник не опередил вас на другом фланге, не вынудил перейти к обороне. Всегда помнить, в случае потери инициативы, ваш штурм лишь ослабит вашу собственную позицию.
3. До рокировки подготовить штурм двумя-тремя пешечными ходами на той стороне доски, где вы задумали вести наступление. Такие предварительные действия окончательно не выясняют еще вашего плана и ведут к выигрышу драгоценного времени.
4. Во время штурма внимательно следить за флангом, где противник штурмует позицию вашего короля. В случае необходимости, сделать там 1-2 оборонительных хода, чтобы задержать продвижение вражеской армии.
5. Сделать полный расчет пешечного штурма, так как его проведение требует 5-7 ходов для вскрытия вертикалей.
При игре с разносторонними рокировками, путей к отступлению нет — точность расчета становится решающим фактором.
Перед рокировкой следует учесть:
1. Положение собственных штурмующих пешек: как далеко они продвинуты, сдвоены они или изолированы, могут ли без больших потерь двинуться с места, не ослабит ли их продвижение позиции ваших фигур.
2. Положение пешек противника. Всякое выдвинутое положение вражеской пешки дает возможность поскорее за нее «зацепиться» и тем самым вскрыть вертикаль. Поэтому обороняющийся обязан избегать продвижения своих пешек навстречу штурмующим отрядам врага, а атакующий — стараться вынудить такое продвижение.
3. Позицию собственных фигур и фигур противника на пути продвигающихся пешек. Чужие фигуры дают лишние темпы — нападая на фигуры пешками, вы заставляете их ходить; свои отнимают время, затраченное на отвод мешающих фигур. Поэтому перед рокировкой в разные стороны, вы обязаны отвести с пути своих пешек свои же фигуры.
4. Расположение собственных фигур, способность их поддержать штурм, ворваться в образующийся пролом в позиции. Если ваши фигуры расположены вдалеке от того места, где вы штурмуете, то при прорыве не будете иметь достаточно сил для того, чтобы использовать эту выгоду. Перед началом штурма необходимо тщательно обдумать вопрос о возможности подведения резервов к важнейшему участку доски.
Правила при игре с односторонними рокировками
1. Фигурная атака — нападающий концентрирует на королевском фланге наибольшее число своих фигур, подводя в случае нужды резервы, затем добирается до вражеского короля, используя слабые пункты в его резиденции, или захватывает открытые вертикали и диагонали.
2. Пешечный штурм — только, если центр надежно защищен (стабилизирован) и противник полностью лишен возможности провести там контрудар , полезно бывает подключить к атаке пешки.
План игры
План игры в шахматах должен быть всегда. План должен быть максимально приближен к требованиям позиции, исходить из оценки позиции. Прежде чем составлять план, надо решить вопрос, какой план у соперника. В комбинационно-тактических позициях следует заняться расчетом вариантов. В маневренно-стратегических позициях — формулированием общих планов и соображений.
Не перегружать себя непосильными планами. Следует изучать типичные планы. Лучше плохой план, чем вообще играть без плана.
При поиске лучшего хода следует выяснить: выполняет ли этот ход намеченную вами цель, не вносит ли диссонанс в расположение всех фигур, не может ли неприятель использовать слабые стороны этого хода для нанесения опасного встречного контрудара.
Прежде чем атаковать, надо хорошо, удачно расставить свои фигуры, ослабить поля противника.
Перед одинокой пешкой противника удобно ставить коня, слона.
При сильном пешечном центре, надо при возможности продвигать пешки, или атаковать на флангах. Если есть проходная, защищенная пешка и ее нельзя двигать, то надо начинать атаку на другом фланге, отвлечь силы противника от нее.
Никогда не следует делать пешечные ходы на том фланге, где вы слабее.
При клинообразном пешечном построении, надо его подорвать пешками же.
При решении вопроса о правильности жертвы надо учитывать:
1. Корректна ли жертва.
2. Попытаться подтвердить сделанный вывод расчетом главных вариантов, получающихся после жертвы.
3. Перед тем, как сделать ход, необходимо оценить другие, более спокойные пути игры. Может быть они короче и вернее ведут к победе.
4. Характер и стиль партнеров. Кому по стилю выгодна жертва: вам или ему? Если он любит комбинационную игру, а вы — спокойную, стоит воздержаться от жертвы. Если вам достаточно ничьи, зачем рисковать.
Защита
1. Не увлекаться атакой. Уметь вовремя понять, что пришла пора обороняться. Иметь чувство опасности.
2. Обороняясь, создавать максимальное число заслонов на пути вражеских фигур, рассчитывая, что это замедлит темп их наступления и застопорит всю атаку. Затем перехватить инициативу.
2. Обороняясь, стремиться к разменам фигур (особенно активных фигур противника), перевести игру в эндшпиль (ладейный или с разноцветными слонами).
3. При запертом центре, кони сильнее слонов.
4. Если у противника один слон, надо попытаться заставить его передвинуть пешки на клетки цвета слона.
5.
Лучший способ обороны — контратака. Главное — найти способ перейти в контратаку и правильно выбрать момент.
6. Лучшее возражение на фланговую атаку — контрудар. Наступление на одном фланге часто без труда отражается противником, особенно если у атакующего нет необходимых пунктов для вторжения фигур. Поэтому надо затеять игру на другом конце доски, отвлекая фигуры между флангами.
Эндшпиль
1. Не спешить: а) выигрываешь время, б) выяснить позицию, повторять ходы, в) усложнять, нагнетать напряжение в позиции с соперником, которому это не нравится.
2. Иметь план, схему конечной позиции.
3. Короля — в центр. Король должен быть активным.
4. Правильно обменять легкие фигуры, выяснив слон дороже или дешевле коня будет в конце игры.
5. При хорошем взаимодействии фигур, при возможности их легко перебрасывать с фланга на фланг, целесообразно вскрывать игру на двух флангах и атаковать одновременно.
6. В ладейных окончаниях, инициатива намного весомее, чем материальное преимущество.
7. Открытые линии имеют ценность в тех случаях, когда на них есть объекты для атаки или когда линия служит коммуникацией для переброски фигур (обычно ладей) к главному участку боя.
Правила обращения с шахматными часами
Наше время — расчет вариантов.
Его время — решение общих проблем, анализ и оценка позиции, составление плана игры.
steptosleep.ru
Ценность фигур. Основы стратегии при обучении шахматам
Ценность фигур. Основы стратегии.
- При спокойном развитии событий сильнейшей фигурой является ферзь, поскольку он движется в любом направлении и на любое расстояние. Конь примерно равен по силе слону, но зато ладья несколько сильнее слона и явно превосходит коня.
- Два коня и слон примерно равны ферзю, а два слона и конь чуть сильнее ферзя.
- Две ладьи по силе превосходят ферзя, но только если они расположены на активных позициях и действуют согласованно.
- Три пешки примерно компенсируют потерю коня, четыре — слона, пять — ладьи и девять — ферзя. Король не может быть взят (мат означает конец игры), поэтому его нельзя оценить.
- Пешка, пересекшая экватор (середину доски), приобретает льготу: при желании она может забрать вражескую пешку после того, как последняя сделает разрешенный в начальной позиции «двойной шаг». При этом атакующая пешка становится на воображаемое поле, где была бы пешка, если бы сделала «одиночный шаг», а сама неприятельская пешка снимается с доски. Этот прием называется «взятие на проходе» и действует только сразу после «двойного хода».
- Достигнув последнего ряда, пешка обязана уйти с поля боя, оставив вместо себя по выбору играющего одну из фигур того же цвета — ферзя, ладью, слона или коня, независимо от того, какое количество указанных фигур уже имеется на доске.
- Если на доске отсутствуют пешки, а у соперника остается одинокий король, то ему легко объявить «шах и мат» с помощью одного ферзя или одной ладьи, чуть сложнее с помощью двух слонов, очень трудно с помощью слона и коня и невозможно двумя конями.
- «Домик короля» можно разрушить в три приема: сначала фигурной атакой ослабить пешечное прикрытие, затем движением пешек создать брешь в обороне и, наконец, организовать решающий штурм и вторжение фигур.
- Атаку противника всегда можно успешно отбить или ослабить, если аккуратно выменивать атакующие фигуры.
- Не следует вести игру только одной полюбившейся вам фигурой, надо искать такой план действий, при котором фигуры попеременно входят в бой, образуя единый ансамбль в атаке и защите. Целесообразно начинать партию с развития легких фигур.
- На первом этапе обучения пешки вокруг короля желательно не трогать вовсе, зато пешки в центре и на другом фланге полезно толкать вперед, создавая больше простора для своих фигур и отнимая безопасные поля у фигур соперника.
- По мере исчезновения с доски сильных фигур роль вашего короля возрастает, так как ему некого бояться. А когда остаются одни только пешки, король смело может (и обязан) идти и атаковать ключевые поля шахматной доски, словом, двигаться в любом направлении: если надо, то к пешкам противника, если надо — на поддержку своих пешек.
- С уменьшением числа фигур возрастает роль пешек, поэтому следует с осторожностью относиться к пешечным разменам.
- Пешки сами в силах пробить любую защитную стенку, так что зря отдавать их не стоит.
- Ради скорой атаки можно иногда поступиться пешкой, а в исключительных случаях для выигрыша лишнего хода не пожалеть коня или слона.
- Ради вскрытия диагонали для слона или вертикали для ладьи бывает полезно пожертвовать пешку.
- Только в том случае, когда можно ясно увидеть позицию с матовым финалом, надо набраться смелости и безбоязненно жертвовать ладью, а то и ферзя.
- Не следует продолжать игру в позиции, в которой у вас, по вашей личной оценке, нет реальных шансов на спасение. Лучше поскорее признайте свой проигрыш, поздравьте соперника с победой и тотчас предложите ему сыграть новую партию. Другими словами, не дожидайтесь мата вашему королю.
- Изучить дебюты только по книжке невозможно, зато, сочетая практическую игру с изучением теории, можно постепенно понять основные стратегические планы и тактические замыслы, спрятанные за «странными начальными ходами» бесконечного числа рекомендованных учебниками дебютных вариантов, взятых из турнирных партий известных мастеров и гроссмейстеров.
chesslabyrinth.ru
Что сколько и почем в шахматах? » Шахматный информационный ресурс
Абсолютная сила
Находясь в центре поля в одиночестве, каждая фигура имеет свою абсолютную силу. Так сказать – это когда в поле войн всего один. Но один он, конечно, никогда не бывает. Оценка стоимости срубленных фигур даёт возможности понять за кем преимущество. Это только материальный расчёт, он не даёт всей полноты оценки. Итак, в классическом варианте абсолютная стоимость фигур рассчитывается таким образом:
пешка – 1 балл;
слон – 3 балла;
конь – 3 балла;
ладья – 5 баллов;
ферзь – 10 баллов;
король – не котируется.
Положим, белые срубили 3 пешки, одного слона и ладью, а чёрные смогли выбить 2 пешки и две ладьи, за кем же преимущество? Давайте посчитаем:
Белые получили 3*1+1*3+1*5=11 очков. Чёрные имеют 2*1 +2*5=12 очков. В плане очков преимущество за чёрными. Всё сильно поменяется, когда мы увидим реальное положение фигур на доске. Вполне возможно, что белые пожертвовали обе ладьи для того, чтобы следующим ходом сделать мат чёрному королю.
Подвижность фигур
Давайте посмотрим немного дальше и оценим также подвижность фигур.
Итак, пешки могут ходить в направлении от 1 до 3, при этом число возможных ходов колеблется от 1 до 4.
Конь может иметь от 2 до 8 видов ходов и столько же направлений. Слон в этом плане более подвижен – ведь он ходит сразу от 7 до 13 клеток, выбирая от 1 до 4 направлений. Поэтому он сильнее коня, но слон ходит лишь по клеткам одного цвета, а конь нет. К тому же конь умеет перепрыгивать через фигуры. Ладья выбирает всегда из 14 ходов, от 2 до 4 направлений.
Ферзь в центре поля – это огромное преимущество. Находясь здесь, он контролирует сразу 27(!) клеток. Даже в углу площадки он может идти в одном из 3 направлений. Король бесценен, при его потере всё прекращается, однако он также может атаковать. При этом его сила оценивается в 4 балла.
Когда пешка сильнее ферзя
Гению шахмат легко добиться того, что пешка превратиться в ферзя и резко повысится в цене, но и в позиционной партии бывает так, что ценность пешки резко возрастает, благодаря её местонахождению на поле. Нужно понимать, что фигуры расположенные в центре доски всегда ценнее фигур, которые стоят на краю площадки. Если игрок контролирует 4 центральных клетки, то партия, скорее всего, закончится в его пользу.
Поэтому старайтесь создать для слона оперативный простор, подвинув пешки для этого. Коня желательно поместить в центр площадки. Развивайте ладью и давайте ей возможности быстрее вступиться в игру, держите ферзя ближе к центру, но всегда держите под контролем уязвимые места, ведь его потеря может оказаться роковой для всей партии.
chess-portal.net
Название фигур в шахматах с картинками и фото
Если вы решили научиться играть в шахматы, первых делом стоит разобраться с названием шахматных фигур. Это значительно ускорит и упростит процесс дальнейшего обучения. Игра в шахматы является одной из древнейших, ей уже много веков. Ее развитие было непрерывным: вначале люди играли зернышками, затем — шариками из глины, и только к Средним векам на доске появились те фигуры, которые знакомы нам.
Сегодня во время игры в шахматы каждый игрок использует шесть видов фигур. Они различаются по цвету: у одного белые фигуры, а у второго — черные. При этом «армия» и одного, и другого игрока состоит из 16 фигурок. Их мы рассмотрим подробнее чуть дальше. У каждой фигурки есть свое место на доске и определенная траектория движения, способ или способы перемещения во время игры. Итак, давайте разбираться с названием фигур в шахматах по картинкам и фото.
1. Король (King) — это самая главная фигура на «поле боя», вокруг которой и строится игра. Ведь конец игры наступает именно тогда, когда повержен король соперника. Несмотря на свой статус, король довольно ограничен в перемещениях, он может передвигаться всего на одну клеточку в любую сторону. Но при этом у него есть преимущество — возможность рокировки. Этот термин означает совместный ход с ладьей, в ходе которого король отправляется в более безопасно место.

2. Ферзь (Queen) — это самая активная, сильная и вторая по значимости фигура во время игры. Ее возможности в траекториях движения наиболее разнообразны. Ферзь может ходить как вверх и вниз по доске, так и влево и вправо, а также и по белым, и по черным диагоналям. Королева — тяжела фигура с точки зрения противника, ведь она обладает большими возможностями для защиты короля и практически в любой момент может оказаться в нужном месте. Выглядит ферзь обычно почти так же, как и король, но немного ниже и с часто с небольшим шариком на верхушке.
3. Ладья (Rook) — эта фигурка двигается только вертикально или горизонтально и ограничена препятствиями. На старте у игрока есть две ладьи, которые размещаются по краям поля. Иногда их называют «офицерами», ведь эти фигурки защищают королевскую семью.
4. Слон (Bishop) — тоже парная фигура, считается легкой, обычно выглядит как невысокая башенка с заостренной капелькой. Эта форма может напомнить одежды монаха — так оно и есть. Появилась фигурка именно благодаря тому, что католические священники увлекались шахматами и привнесли в нее что-то свое.
5. Конь (Knight) — обычно выглядит, как соответствующее животное. Его особенность — необычная манера передвижения, а именно буквой «Г» в любую сторону. Конь легко перепрыгивает через препятствия (фигуры соперника) и в начале игры стоит рядом с ладьей.
6. Пешка (Pawn) — это шахматный солдат, который первым рвется в бой, открывает игру. У каждого есть по 8 пешек. Ходят они наиболее просто — по одной клеточке и только вперед, хотя в качестве первого хода могут перепрыгнуть через клеточку, — а сбивают вражеские фигурки только наискосок. Пешки играют важную роль, они обороняют другие фигуры, а дойдя до противоположного края доски могут вернуть вместо себя любую сбитую ранее фигурку — и ферзя, и ладью, и коня. Исключение здесь составляет только король.
(8420)
chess-boom.online

 С точки зрения общей теории слона и коня следует считать одинаково ценными, хотя, по моему убеждению, слон в большинстве случаев оказывается более сильной фигурой. Между тем считается вполне установленным, что два слона почти всегда сильнее двух коней.
С точки зрения общей теории слона и коня следует считать одинаково ценными, хотя, по моему убеждению, слон в большинстве случаев оказывается более сильной фигурой. Между тем считается вполне установленным, что два слона почти всегда сильнее двух коней. Стратегия игры в шахматы
Стратегия игры в шахматы